DualConvMesh-Net: Joint Geodesic and Euclidean Convolutions on 3D Meshes

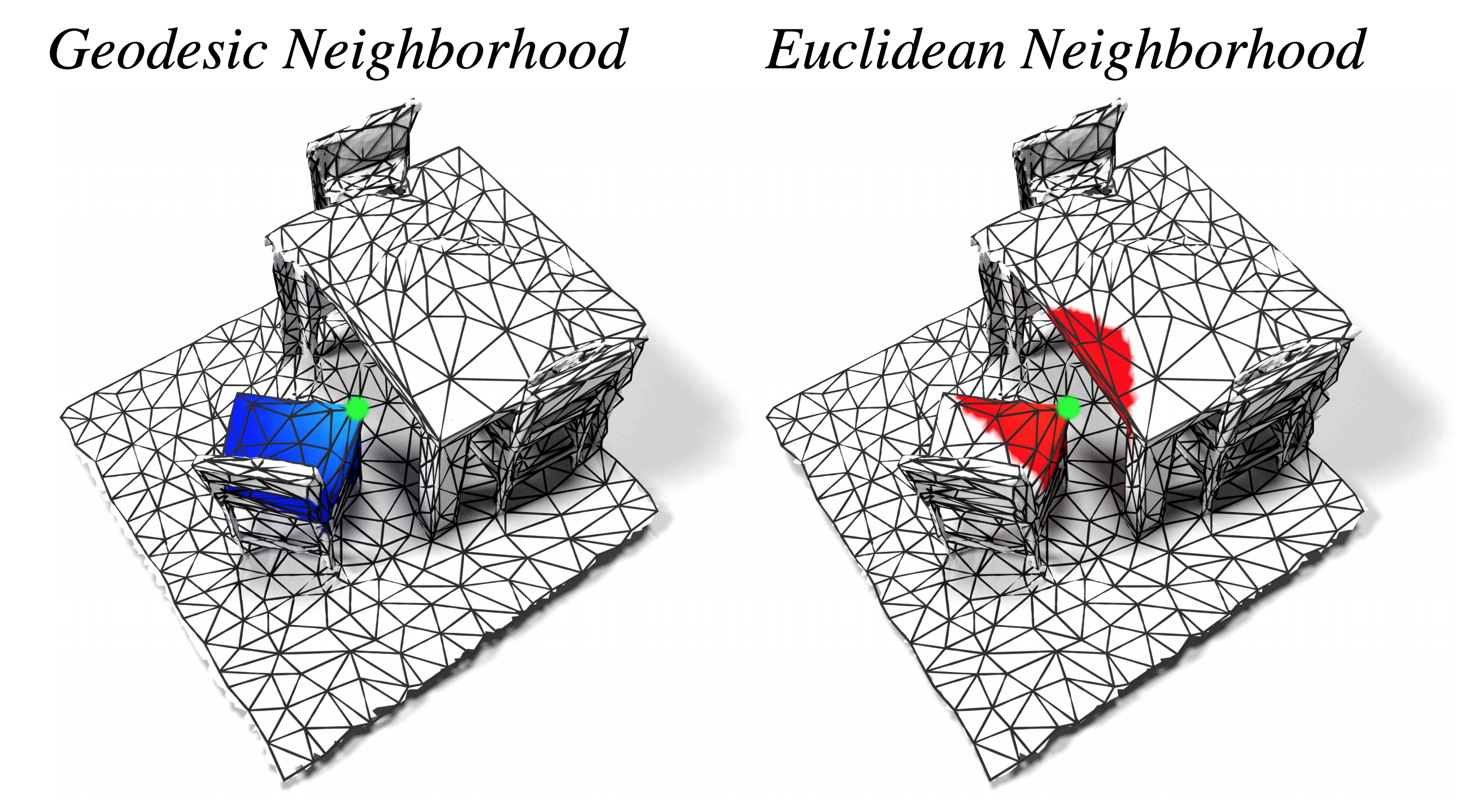
We propose DualConvMesh-Nets (DCM-Net) a family of deep hierarchical convolutional networks over 3D geometric data that combines two types of convolutions. The first type, geodesic convolutions, defines the kernel weights over mesh surfaces or graphs. That is, the convolutional kernel weights are mapped to the local surface of a given mesh. The second type, Euclidean convolutions, is independent of any underlying mesh structure. The convolutional kernel is applied on a neighborhood obtained from a local affinity representation based on the Euclidean distance between 3D points. Intuitively, geodesic convolutions can easily separate objects that are spatially close but have disconnected surfaces, while Euclidean convolutions can represent interactions between nearby objects better, as they are oblivious to object surfaces. To realize a multi-resolution architecture, we borrow well-established mesh simplification methods from the geometry processing domain and adapt them to define mesh-preserving pooling and unpooling operations. We experimentally show that combining both types of convolutions in our architecture leads to significant performance gains for 3D semantic segmentation, and we report competitive results on three scene segmentation benchmarks.